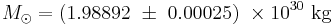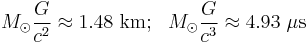Solar mass
The solar mass (M☉), 1.98892×1030 kg, is a standard way to express mass in astronomy, used to describe the masses of other stars and galaxies. It is equal to the mass of the Sun, about two nonillion kilograms or about 332,950 times the mass of the Earth or 1,048 times the mass of Jupiter.
The solar mass can be determined from the length of the year, the distance of the Earth to the Sun (the astronomical unit) (AU), and the gravitational constant (G) as
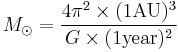 .
.
The value of the gravitational constant was derived from 1798 measurements by Henry Cavendish using a torsion balance. The value obtained differed only by about 1% from the modern value.[2] The diurnal parallax of the Sun was accurately measured during the transits of Venus in 1761 and 1769,[3] yielding a value of 9″ (compared to the present 1976 value of 8.794148″). When the value of the diurnal parallax is known, the distance to the Sun can be determined from the geometry of the Earth.[4]
The first person to estimate the mass of the Sun was Isaac Newton. In his work Principia, he estimated that the ratio of the mass of the Earth to the Sun was about 1/28,700. Later he determined that this value was based upon a faulty value for the solar parallax, which was used to estimate the distance to the Sun (1 AU). He revised his result to obtain a ratio of 1/169,282 in the third edition of the Principia. The current value for the solar parallax is smaller still, giving the correct mass ratio of 1/332,946.[5]
Until recently, neither the AU nor the gravitational constant was precisely measured. However, a determination of the relative mass of another planet in the Solar System or of a binary star in units of solar masses does not depend on these poorly known constants. So it was useful to express these masses in units of solar masses (see Gaussian gravitational constant).
The mass of the Sun changes slowly, compared to the lifetime of the Sun. Mass is lost due to two main processes in nearly equal amounts. First, in the Sun's core hydrogen is converted into helium by nuclear fusion, in particular the pp chain. Thereby mass is converted to energy in correspondence to the mass–energy equivalence. This energy is eventually radiated away by the Sun. The second process is the solar wind, which is the ejection of mainly protons and electrons to outer space.
Contents |
Related units
One Solar mass can be converted to related units:
- 27068510 Lunar mass (ML)
- 332946 Earth mass (M⊕)
- 1047.56 Jupiter mass (MJ)
It is also frequently useful in general relativity to express mass in units of length or time.
See also
|
|
References
- ↑ Castellani, V.; Degl'Innocenti, S.; Fiorentini, G.; Lissia, M.; Ricci, B. (March 1997). "Solar neutrinos: beyond standard solar models". Physics Reports 281 (5-6): 309–398. doi:10.1016/S0370-1573(96)00032-4. This cites the Astronomical Almanac for the Year 1994.
- ↑ Holton, Gerald James; Brush, Stephen G. (2001). Physics, the human adventure: from Copernicus to Einstein and beyond (3rd ed.). Rutgers University Press. p. 137. ISBN 0813529085.
- ↑ Pecker, Jean Claude; Kaufman, Susan (2001). Understanding the heavens: thirty centuries of astronomical ideas from ancient thinking to modern cosmology. Springer. pp. 291–291. ISBN 3540631984.
- ↑ Barbieri, Cesare (2007). Fundamentals of astronomy. CRC Press. pp. 132–140. ISBN 0750308869.
- ↑ Leverington, David (2003). Babylon to Voyager and beyond: a history of planetary astronomy. Cambridge University Press. p. 126. ISBN 0521808405.
Further reading
- I.-J. Sackmann, A. I. Boothroyd (2003). "Our Sun. V. A Bright Young Sun Consistent with Helioseismology and Warm Temperatures on Ancient Earth and Mars". The Astrophysical Journal 583 (2): 1024–1039. doi:10.1086/345408. http://adsabs.harvard.edu/abs/2003ApJ...583.1024S.
|
||||||||||||||||||||||||||||||||||||||||||||